PowerPoint sunumunu indirmek için lütfen tıklayınız:
PDF formatında indirmek için lütfen tıklayınız:
Matematiksel Düzen ve Çoklu Zeka Kuramı Proje Görevi
«Evren, dünyamız ve varlıklar matematiksel bir düzen içerisinde tasarlanmıştır.»
Bu konuda çoklu zeka kuramından birini seçerek aşağıdaki çoklu zeka ile iligili verilen örneklere uygun proje görevini yapınız.
Alternatif olarak kendi seçeceğiniz başka örnekler de kullanarak projenizi hazırlayabilirsiniz.


Mantıksal-Matematiksel Zeka:
Matematiksel hesaplama, mantıksal düşünme, problem çözme becerileridir.

Günlük hayatta karşılaşılan matematiksel problemlere örnekler verilerek ve problemler çözülerek konu açıklanır.
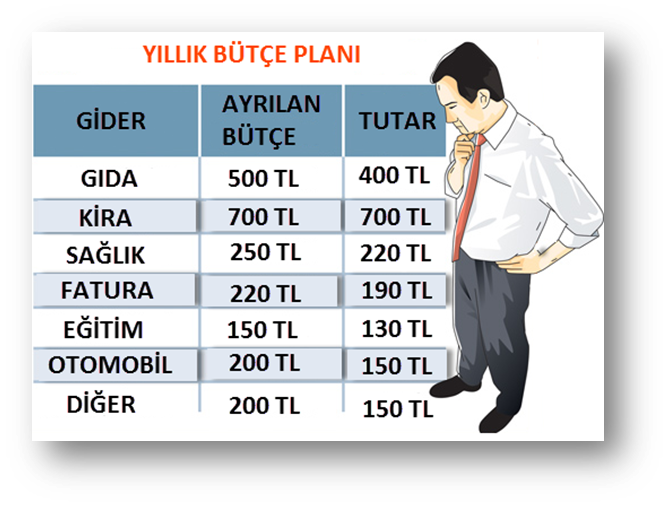
Örneğin:
Aile bütçesinin hesaplanması,
Gelir – gider tablosu
Kar – zarar durumu
Alışveriten sonra kalan para miktarı, para üstü vb.
Doğa Zekası:
Doğal çevreyi anlama, analiz etme ve onunla ilişki kurma becerisidir.
Doğadan ve doğadaki varlıklardan matematiksel hesaplamalar ve örnekler vererek konu açıklanır.

Örneğin:
Nesli tükenmek üzere olan hayvanların sayısı ve onlarla ilgili yapılan çalışmalarda matematiksel olarak ilerleme olup olmadığı,
Yıllık üreme ve ölüm dengesinin karşılaştırılması, canlı türünün devam edip edemeyeceği hakkında yorum yapma.
Dilsel (Sözel-Dilsel) Zeka:
Sözcüklerle etkili bir şekilde düşünme ve ifade etme becerisidir.
Evren, dünyamız ve varlıkların matematiksel bir düzen içerisinde tasarlanması hakkında çeşitli örneklerle bir sunum hazırlanır ve sınıfa ya da hedef kitleye sözel olarak sunulur.

Örneğin:
Evrenin, dünyamızın ve varlıkların yaratılmasında harika bir matematiksel işlemler kullanıldığı;
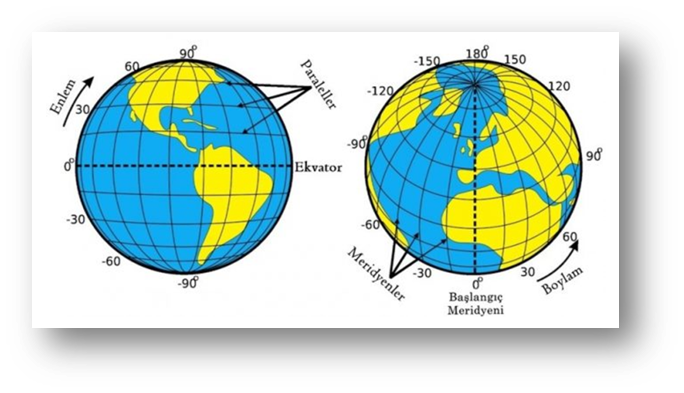
- bunun atom, moleküller, elementler, hücreler, canlılar,
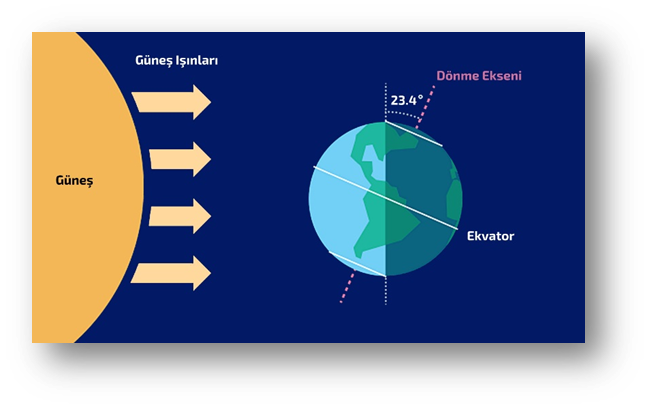
- coğrafi konumlar, dünyanın şekli ve güneş sistemindeki konumu,
- matematiksel olarak nasıl eğik durduğu,
- bunun mevsimlerin uluşturulmasındaki etkisi,
- güneş sisteminin samanyolu galaksisindeki yeri,
- yıldızlar ve yıldız kümeleri ve burçlardan örnekler
verilerek bütün bunların tesadüfen ya da kendi kendine olamayacağı ya da bilinçsiz tabiat tarafından yapılamayacağı bilimsel ve matematiksel ifadelerle anlatılır ve sunulur.
Görsel-Mekânsal Zeka:
Görsel bilgileri anlamak, analiz etmek ve zihinde hayal etme becerisidir.
Örneğin;
Altın oran gibi matematiksel ve görsel örneklerden bir sunum hazırlanır ve sunulur.

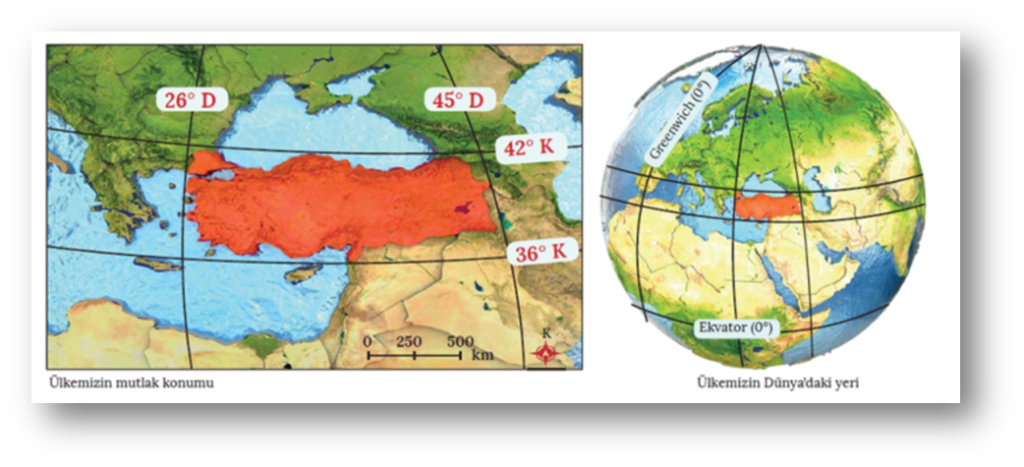
Alternatif olarak dünyamızın matematiksel konumu ya da yaşadığınız yerin coğrafi konumunun matematiksel ve görsel olarak hesaplanması yapılarak görsellerle açıklanır.
Bedensel-Kinestetik Zeka:
Fiziksel hareketleri kullanma, kontrol etme ve ifade etme becerisidir.
Matematik kullanılarak grupla oynanabilen hareketli bir oyun seçilerek grup halinde oynanır. Oyunun kuralları ve matematiksel ifadeler açıklanır.

Örneğin;
Sınıf 10 ar kişilik gruplara ayrılır. Kalan öğrenciler hakem ve juri olur. Öğretmen ya da moderatör talimat verince gruplar ona göre hareket eder.
Grubun 1/10 öne çıksın der. Gruptan bir kişi öne çıkması gerekir. Doğru yapılırsa oyun devam eder. Yanlış yapan grup oyunu kaybeder.
Örneğin grubun ½ si öne çıksın denilince 5 kişinin öne çıkması gerekir. Bu sayıdan faklı kişi öne çıkarsa o grup kaybeder.

Alternatif olarak 19 Mayıs hareketleri ve stadyumdaki gösterilerde matematiksel düzene benzer hareketler uygulanır.

Müziksel Zeka:
Ritmi, melodiyi ve müzikal yapıları anlama ve oluşturma becerisidir.
Müzikle matematik arasındaki ilişki uygulamalı olarak icra edilir ve açıklanır.

Örneğin:
Çalınacak müzik aleti ya da okunacak müziğin notaları getirilir.
Müzk aletinin matematiksel yapısı incelenir,
Kaç nota olduğu ve bunların dizilişi ya da örüntüsü üzerinde konuşulur.
Anlatılanlar bir müzik aletiyle ya da ses verilerek icra edilir.

Kişilerarası Zeka:
Başkalarıyla etkili bir şekilde iletişim kurma ve empati yapma becerisidir.
Ekonomi, gelir-gider dengesi, enflasyon ve sosyal olaylar arasında ilişkiler kurar, politikacıların aldığı kararların matematiksel olarak topluma nasıl yansıdığı açıklanır. Bu zeka alanını seçenler grup olarak da çalışabilir.

Örneğin:
Dünyada, ülkede, şehirde, kasaba ya da köyde, ailede yaşayan insan sayısı
Ülkenin ekonomik durumu iç borç – dış borç ve bunun topluma yansıması
Merkez bankasının faiz oranlarında artış ya da azqltma kararının etkileri
Gelir dağılımındaki adaletsizlik ve bunun sosyal patlamalara sebep olması
bunların matematiksel olarak ifadesi

İçsel (Kişisel) Zeka:
Kendi duygularını, düşüncelerini anlama ve değerlendirme becerisidir.
Matematiksel düzen hakkındaki kendi duygu ve düşüncelerini deneme, makale, şiir ya da kompozisyon şeklinde bir metin halinde ifade eder.

Örneğin:
Matematik nedir, ne işimize yarar?
Matematiksel bir düzen olmasaydı hayat nasıl olurdu?
Matematik eğitimi zor mu, kolay mı? Neden?
gibi sorulara kendi düşünceleri noktasından yaklaşarak gerekçeleriyle açıklar.

KAYNAKÇA
https://www.multikidsakademi.com/coklu-zeka-kurami-ile-matematik-ogrenme
https://firmajans.com.tr/dijital-pazarlama/dijital-pazarlamada-matematiksel-modelleme/
https://kumbaradergisi.com/icerikler/sayilar-oymasaydi-ne-olurdu/
https://fatihturgut.com.tr/peteklerin-neden-altigen-oldugunu-biliyor-musunuz/
https://www.matematiksel.org/altin-oran-nedir-ne-degildir/
https://egitimpedia.com/ogretmen/grup-tartismalarinin-avantajlari-ve-dezavantajlari/